Bathymetry smoothing
 The depth of many seas, particularly in the Adriatic Sea, has the inconvenience of varying too much for realistic oceanic modelling. The problem showed up in the computation of pressure difference in terrain following models. When the depths vary too much, artificial currents occur which compromise the stability of the model.

Raw depth of the Adriatic Sea

Region of hydrodynamic stability (in blue) and instability (in red).
So, it is necessary to smooth the bathymetry in oceanic models, but one wants to use a bathymetry, which is as near as possible as the real one. We proposed a new linear programming method which performs much better than existing methods. 		L M. Dutour Sikirić, I. Janeković, M. Kuzmić, A new approach to bathymetry smoothing in sigma-coordinate ocean models, Ocean Modelling 29 (2009) 128- -136.
Space fullerenes
 A space fullerene is a tiling of Euclidean space by fullerenes. Such tilings occur in Metallurgy, Crystallography, Soap froth, Optimization problems, etc. I enumerated small space fullerenes




LM. Dutour Sikirić, O. Delgado-Friedrichs, M. Deza, Space fullerenes: computer search for new Frank-Kasper structures, Acta crystallographica A 66 (2010) 602--615.
LM. Dutour Sikirić, M. Deza, Space fullerenes: computer search for new Frank-Kasper structures II, Structural Chemistry 23-4 (2012) 1103--1114.
Coupling of circulation and wave models
 I coupled the circulation model ROMS with the wave model WWM. Below the effect of coupling:




The coupling makes the significant wave height lower in the Bura jet but increases it in front of Istria. 		L M. Dutour Sikirić, A. Roland, I. Tomažić, I. Janeković, Hindcasting the Adriatic Sea near-surface motions with a coupled wave-current model, Journal of Geophysical Research - Oceans, 117 (2012) C00J36.
LM. Dutour Sikirić, A. Roland, I. Janeković, I. Tomažić, M. Kuzmić, Coupling of the Regional Ocean Modelling System and Wind Wave Model, Ocean Modelling 72 (2013) 59--73.
Geometry of Numbers
 A lattice L is a discrete subgroup set of the Euclidean space In a lattice L an empty sphere is a sphere containing no lattice points in its interior and containing n+1 affinely independent points on its surface. A Delaunay polytope is the convex hull of the points on the surface of an empty sphere.

Delaunay polytopes in a 2D lattice

Voronoi polytopes in a 2D lattice
Delaunay polytopes form a tesselation dual to the Voronoi partition, which has a lot of uses in computational geometry and physics. We design specific algorithm for enumerating the Delaunay polytopes under symmetry. 		L M. Dutour Sikirić, A. Schuermann, F. Vallentin, Complexity and algorithms for computing Voronoi cells of lattices, Mathematics of computation 78 (2009), 1713--1731.
Combinatorial types
 The 3-dimensional lattice Delaunay polytopes have been classified by E. Fedorov in 1885 (see below). I enumerated them in dimension 6.
2 2 Dirichlet (1860)
3 5 Fedorov (1885)
4 19 Erdahl-Ryshkov (1987)
5 138 Kononenko (1997)
6 6241 Dutour (2004)
L M. Dutour, The six-dimensional Delaunay polytopes, European Journal of Combinatorics 25 (2004) 535--548.
Perfect Delaunay polytopes
 If the only deformation preserving a lattice Delaunay polytope are the isometries and homotheties, then it is called perfect. Such polytopes correspond to the extreme rays of a polyhedral cone, named the Erdahl cone. I created an infinite series of extreme Delaunay polytope, which generalize the classical Schafli polytope. Furthermore I introduced classical techniques of combinatorial optimization in this subject, which allowed us to find 2, 27 extreme Delaunay polytopes in dimension 7 and 8, respectively. 		L M. Deza, M. Dutour, The hypermetric cone on seven vertices, Experimental Mathematics 12 (2004) 433--440.
L M. Dutour, Infinite Serie of Extreme Delaunay polytope, European Journal of Combinatorics 26 (2005) 129--132.
L M. Dutour, Adjacency method for extreme Delaunay polytopes, Voronoi's Impact on Modern Science, Book 3, 94--101.
L M. Dutour Sikirić, K. Rybnikov, Delaunay polytopes derived from the Leech lattice, preprint.
L-type domains and the lattice covering problem
 A family of balls of equal radius such that every point belongs to at least one ball is called a covering; its density is the average number of balls to which points belongs to. See below a 2-dimensional covering:

Every lattice determines a partition of the space into Delaunay polytopes. L-type domains are combinatorial type of Delaunay tesselations of the Euclidean space. When, one knows the Delaunay polytopes of a lattice, it becomes possible to compute its covering density, i.e. the density of a covering of space with balls centered on the lattice. Using semidefinite programming one can optimize the covering density over a L-type and solve the lattice covering problem in a fixed dimension, if one knows all the L-type domains. In practice this is possible only up to dimension 5. Using a generalization of L-type, we were able to find record lattice coverings in dimension 9 to 15 and to classify the totally real thin algebraic number fields. 		L A. Schuermann, M. Dutour Sikirić, F. Vallentin, A generalization of Voronoi's reduction theory and its application, Duke Math. J. 142 (2008), 127--164.
Polyhedral computation with symmetry
 The programs lrs and cdd allow to compute the dual description of a polytope. Unfortunately, in many cases, we cannot apply them for memory and time reasons. Starting from the Adjacency Decomposition method of Christof & Reinelt I progressively build an extremely good algorithm for computing dual description of polytopes with symmetry.
  • Perfect forms are prominent object in the geometry and number theory of quadratic form. We computed all perfect forms in dimension 8 and found 10916 of them, a technical feat deemed impossible before. The main challenge was the computation of all facets of a polyhedral cone in dimension 36 with 120 extreme rays. It has about 25,075,566,937,584 facets which fall into 83,092 orbits.

  • The Leech lattice is the most remarkable lattice of geometry of numbers. We determine the facets of its contact polytope. There are 1,197,362,269,604,214,277,200 facets in 232 orbits.
 L D. Bremner, M. Dutour Sikirić, A. Schuermann, Polyhedral representation conversion up to symmetries, CRM proceedings, volume 48.
L M. Dutour Sikirić, A. Schuermann, F. Vallentin, Classification of eight dimensional perfect forms, Electron. Res. Announc. Amer. Math. Soc. 13 (2007), 21--32.
L M. Dutour Sikirić, A. Schuermann, F. Vallentin, The contact polytope of the Leech lattice, submitted.
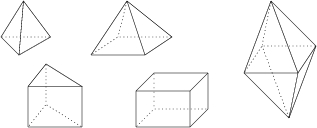
Elementary polycycles and Face regular maps
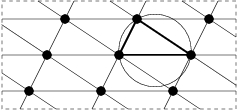
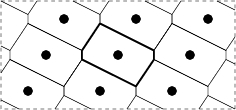
 A (R,q)-polycycle is a plane graph, whose faces, besides some disjoint holes, are i-gons for i in R, and whose vertices, outside of holes, are q-valent. Such polycycle is called elliptic, parabolic or hyperbolic if 1/q + 1/r - 1/2 (where r is the maximum of R) is positive, zero or negative, respectively. Such polycycles can be uniquely decomposed into some simpler elementary polycycles. We classify the elementary elliptic (R,q)-polycycles, i.e. elementary ({2,3,4,5},3)-, ({2,3},4)- and ({2,3},5)-polycycles. This gives a very efficient proof and enumeration technique, which we applied to the enumeration of face regular maps.
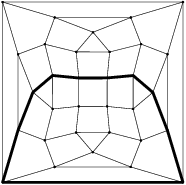
A 3-valent torus or spherical map with p- and q-gonal faces is called pRi (respectively qRj) if every p-gonal (respectively q-gonal) face is adjacent to exactly i p-gonal (respectively j q-gonal) faces. We considered the question of existence, finiteness and classification for those classes of graphs.

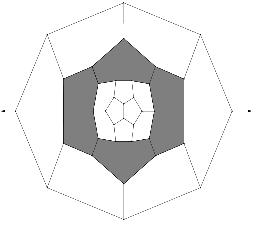
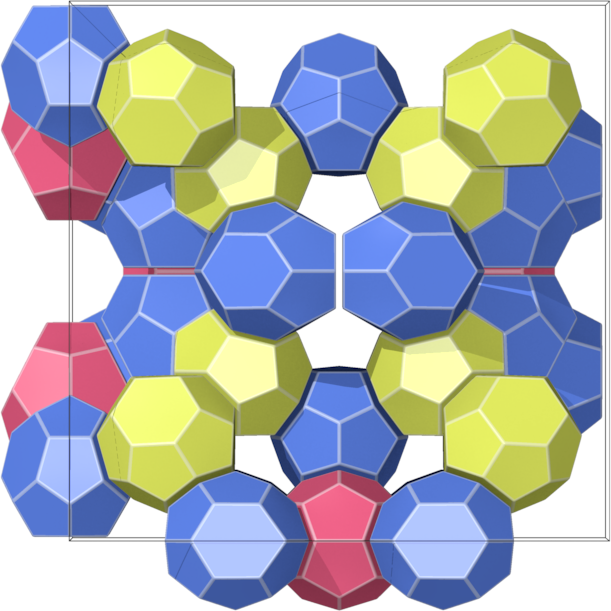
A (5,8)-sphere 8R2

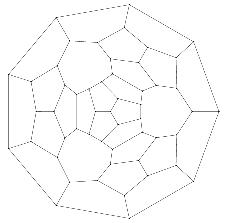
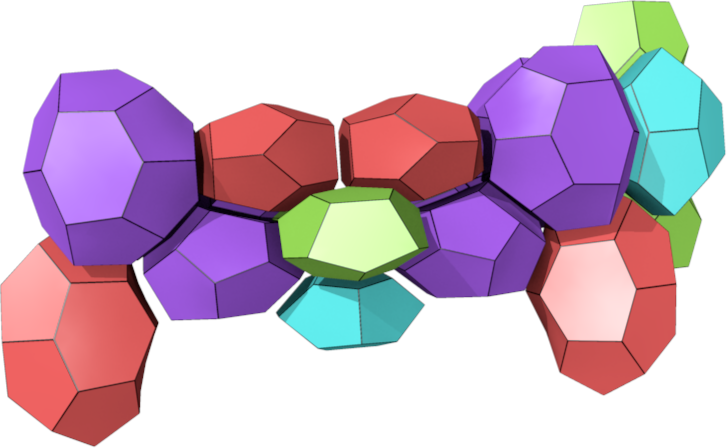
A (5,9)-sphere 9R0
L M. Deza, M. Dutour, M. Shtogrin, Elementary elliptic (R,q)-polycycles, Analysis of Complex Networks, From Biology to Linguistics, edited by M. Dehmer, F. Emmert-Streib, Wiley-Blackwell, Weinheim 2009, 351--376.
L M. Deza, M. Dutour Sikirić, Geometry of Chemical Graphs, Cambridge University Press, Series: Encyclopedia of Mathematics and its Applications (No. 119)
L M. Deza, M. Dutour, M. Shtogrin, Elliptic polycycles with holes, Russian Math. Surveys. 60 (2005) 349--351
Zigzags and central circuits
 We have considered the structure of central circuit (circuit of edges, such that no two consecutive edges belong to the same face) for 4-valent plane graph and zigzags (circuit of edges, such that any two, but no three, consecutive edges belong to the same face) for 3-valent plane graphs. See below two parts of such objects:

Central circuit in a 4-valent plane graph.

Zigzag in a 3-valent plane graph.
Those notions were considered for 3- or 4-valent maps, whose faces have size at most 6 or 4, respectively. We classified the graphs, which are 2-connected but not 3-connected and we give all possible symmetry groups. The invention of railroads, which roughly speaking is two parallel such objects, allowed us to introduce new notions and extremal problems, which led to several classification results.
The Goldberg-Coxeter construction, which takes a 3- or 4-valent plane graph and a pair (k,l) of integers for creating a new 3- or 4-valent plane maps was considered in this context: We computed the zigzag or central circuit structure of the Goldberg construction by creating a new formalism of (k,l)-product and the introduction of a finite index subgroup of SL2(Z). 		L M. Dutour, M. Deza, Goldberg-Coxeter construction for 3- or 4-valent plane graphs, Electronic Journal of Combinatorics 11 (2004) R20.
L M. Deza, M. Dutour, Zigzag Structure of Simple Two-faced Polyhedra, Combin. Probab. Comput. 14 (2005), 31--57
L M. Deza, M. Dutour, P. Fowler, Zigzags, Railroads, and Knots in Fullerenes, Journal of Chemical Information and Computer Sciences 44 (2004) 1282--1293.
L M. Deza, M. Dutour, M. Shtogrin, 4-valent plane graphs with 2-, 3- and 4-gonal faces, "Advances in Algebra and Related Topics" (in memory of B.H. Neumann; Proceedings of ICM Satellite Conference on Algebra and Combinatorics, Hong Kong 2002), World Scientific Publ. Co. (2003) 73--97.
Simplicial complexes
 All simplicial n-complexes, whose (n-2)-dimensional faces are contained in 3 or 4 simplices have been classified in terms of partitions of {1,..., n+1}. See below the 2-dimensional case:

{1,2,3}

{1,2}, {3}

{1}, {2}, {3}
L M. Deza, M. Dutour Sikirić, M. Shtogrin, On simplicial and cubical complexes with short links, Israel J. Math. 144 (2004), 109--124.
Wythoff polytopes
 The Wythoff construction takes a non-necessarily convex n-dimensional polytope P, a non-empty subset S of {0,...,n} and returns another n-dimensional polytope W(P,S). Particular cases are duality, medial polytope, clique clomplex, ... We determined a conjecturally complete list of polytopes W(P,S) that are L1-embeddable for P a regular polytope. The Wythoff construction was also used to compute the third homology group of the Mathieu group M24. 		L M. Deza, M. Dutour Sikirić, S. Shpectorov, Hypercube Embedding of Wythoffians, Ars Math. Contemp. 1 (2008), 99--111
L M. Dutour, G. Ellis, Wythoff polytopes and low-dimensional homology of Mathieu groups, preprint.
Cube packings and tilings
 A cube tiling (respectively packing) is a 4-periodic tiling (respectively packing) of R^n by translates of cubes [-1,1]^n. Much of this research came from the existence in dimension 3 of a non-extensible cube packing with 4 translation classes of cubes:

For example, we prove that any cube packing with more than 2^n-4 cubes are extendible to a cube tiling. We also give lower bounds on the size of non-extendible cube packings. We also consider continuous parametrization of cube packings, which surprisingly are still amenable to combinatorial methods. 		L M. Dutour Sikirić and Y. Itoh, Continuous random cube packings in cube and torus, European Journal of combinatorics, to appear.
L M. Dutour Sikirić, Y. Itoh, A. Poyarkov, Cube packings, second moment and holes, European J. Combin. 28 (2007), 715--725.
Ginzburg Landau model
 My PhD thesis was on the bulk Ginzburg-Landau model of superconductivity. This is a partial differential equation model depending on a structural parameter k and the exterior field Hext. The internal states of the model are described by an interior magnetic field Hint and a complex valued wave function phi. By using the Bochner Kodaira Nakano formula of complex hermitian geometry, I established the classical form of the phase diagram with the pure state region (phi=1 all electron supraconductor), the normal region (phi=0 no electron supraconductor) and the mixed region where both kinds of electron coexist:
I also established the Abrikosov asymptotic expansion in the bifurcated region for the minimal energy and the states realizing it. 		L M. Dutour, Phase diagram for Abrikosov lattice, Journal of Mathematical Physics 42 (2001) 4915--4926.